Non-Newtonian Fluids

Authors : Yash Gandhi, Gaurav Khadke, Shruti Gavare, Chaitanya Gawali, Shreyas Gaware

Types Of Fluids :-

1) Newtonian Fluids

2) Non-Newtonian Fluids

Newtonian Fluids

The fluids which follows Newton law of Viscosity over its all range of shear rates are known as Newtonian Fluids.

Newtons Law of Viscosity

With the change in shear stress or shear rates there is no change in the viscosity of the fluid. The following illustrates the Newton Law of Viscosity.

                                                  τ = µdu/dy

where:

· τ is the shear stress;

· μ is the viscosity, and

· du/dy is the shear rate.

Fluid is Newtonian, if Viscosity is constant.

Figure 1

Examples of Newtonian Fluid : Water, Air, Oil, Alcohol, Organic Solvents, Honey, etc.

Non-Newtonian Fluid

The Fluids which does not obey the Newton Law of Viscosity is Non-Newtonian Fluid. In non-Newtonian fluids, viscosity can change when under force to either more liquid or more solid. Examples of substances exhibiting non-Newtonian Fluid Behavior are Adhesives (wall paper paste, carpet adhesive, for instance), Ales (beer, liqueurs, etc.).

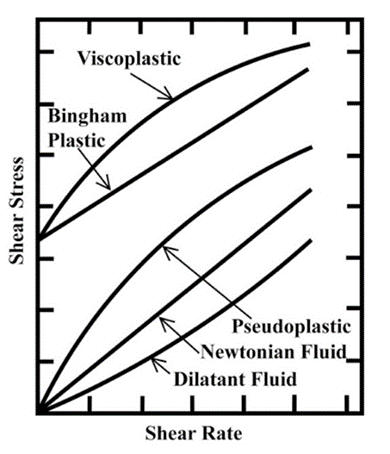
Types Of Non-Newtonian Fluids :

Behavior Of Non-Newtonian Fluid

Figure 2

The simplest possible deviation from the Newtonian fluid behavior happens once the simple shear information σ − γ˙ doesn’t meet up with the origin and/ or doesn’t result into a linear relationship between σ and γ˙. Conversely, the apparent viscosity, outlined as σ/γ˙, isn’t constant and could be a operate of σ or γ˙. Indeed, below acceptable circumstances, the apparent consistency of certain materials isn’t only an operation of flow conditions (geometry, rate of shear, etc.), however it additionally depends on the kinematic history of the fluid element into account. it’s convenient, though arbitrary (and most likely unscientific too), to group such materials into the subsequent three categories:

1. Systems for which the value of ‘γ’ at a point inside the fluid is set only by the present value of σ at that point; these substances are diversely referred to as purely viscous, inelastic, time-independent or generalized Newtonian fluids (GNF);

2. Systems that the relation between σ and γ˙ shows additional dependence on the period of shearing and kinematic history; these are known as time-dependent fluids, and at last,

3. Systems that exhibit a blend of viscous fluid behavior and of elastic solid-like behavior. as an example, this class of materials shows partial elastic recovery, recoil, creep, etc. consequently, these are known as visco-elastic or elastico-viscous fluids.

TIME INDEPENDENT FLUID:

The flow pattern for Time Independent fluid is determined by the following term,

ϒ(yx) =f(τyx)              ………….(1.1)

Or the inverse form is as follows:

(τyx)=  f’(ϒ(yx))         …………..(1.2)

Depending upon the value of shear stress within the sheared fluid at any point determines the value of ϒ at that point. By considering equation 1.1 and 1.2 the fluids are classified in different forms.

(1     1)   Shear Thinning

(2     2)   Visco plastic

(3     3)   Shear Thickening

Shear Thinning

https://images.app.goo.gl/GuwCiYLjrbx14waG8

Figure 3

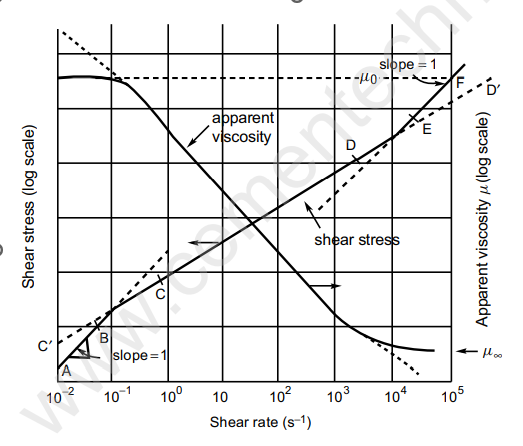
Most commonly known Shear Thinning is Time Independent fluid. In this type of fluid viscosity decreases by increasing the value of shear rate. Most shear thinning polymers as well as melts try to resembles Newtonian fluid at very high and low shear rates. The plots becomes straight lines.

By observing the graph we are able to see that at high shear rates and low shear rates the apparent viscosity tends to zero µ0 and infinite µ∞ respectively. This shows us that viscosity reduces with increasing shear rates.

Figure 4 : Schematic representation of shear-thinning behavior

The above Graph shows the apparent viscosity — shear rate behavior of an aqueous polyacrylamide solution at 273K. Considering the drop of viscosity from 1400 mPa.s to 4.2 mPa.s it is not possible to assign one value to viscosity. The dependency of upper and lower values of viscosity is on the concentration, molecular weight etc. by taking in account all these factors the lower limiting value for viscosity is exhibited below 10^-2 per second and above 10⁵ per second. If the value of molecular weight and concentration of the polymer is reduced it is observed that the range of shear rates for which the viscosity is constant increases

Figure 5

Power Law or Ostwald de Waele Equation

A straight line over a period of shear rate could be a approximate connection between shear stress () and shear rate() shown on log-log co-ordinates for a shear-thinning fluid.

 σ = m(γ˙)^n ………(1)

Alternatively, we can say in the terms of viscosity,

η = m(γ˙)^(n−1)……….(2)

Obviously 0 and n< 1 can generate (dη/dγ˙)0, i.e., H. Liquids consisting Shear Thinning behavior are characterized by a value of n (power law index) which is less than one. various polymer melts and solutions have the value of n in the range of 0.307 depending on the concentration and molecular weight of the polymer etc. Even lower values of the power law index (n ∼ 0.1−0.15) are found in suspensions of fine particles such as kaolin water, bentonite water etc. The smaller is the value of n, the more the material is naturally thinned. The other constant m (consistency index) could be a measure of the consistency of the substance.

Although Eq. (1) or (2) give the simplest approximation to the behavior of shear thinning and predict neither the highest nor the lowest Newtonian plateaus within the limits of γ˙ → 0 or γ˙ → ∞. In addition, the values of m associated with n are moderately constant over a narrow range of shear rate variation from which the possible shear rate variation found in an intended application must be known a priority.

The Carreau viscosity equation :

By taking in consideration the deviation from the power law model at very high and very low shear rates it is necessary to bring The Carreau viscosity equation model.

Carrying the molecular weight networks Carreau presented a model which takes into account both the limiting values of viscosities µ0 and µ∞

µ- µ∞/ µ0- µ∞={1+( Λϒ(yx))²}^((n-1)/2)

where n<1 and Λ are curve fitting parameter. With the expense of complexity of four parameters, this model can show shear thinning pattern over inclusive range of shear rates.

At µ= µ0 and n=1 or Λ=0 or both the model resembles Newtonian fluid pattern.

The Ellis Fluid Model :

Ellis model is appropriate to use when the we observe significant deviations from power-law model but only when shear rates are low. The above mention two models are illustrations of the equation (1.2) where as the equation (1.1) inverse forms illustration is three-constant Ellis Model. Ellis model Fluid apparent viscosity in simple shear is given by :

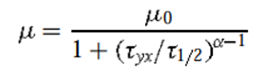…………(1.)

Where ,

µ0 : Zero shear Viscosity

(α and τ1/2) : Adjustable Parameters

Here α is index and it is measure of the degree of shear-thinning behavior thus the extent of shear-thinning is given by α as the value increase the extent of shear-thinning also increases. τ1/2 is shear stress where the apparent viscosity dropped to half of its zero-shear value. In the limit of τ1/2 tending to ∞ Ellis equation predicts the Newtonian fluid behavior. If the stress distribution is known this type of equation permits the easy calculations of velocity profiles this is its advantage but the reverse operations become very heavy and lengthy.

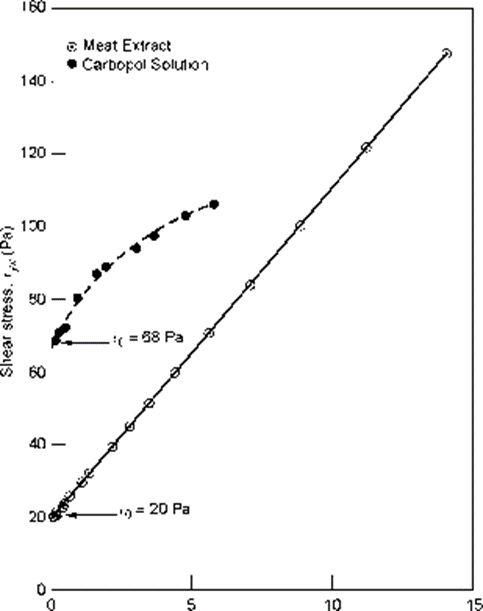
Viscoplastic Fluid Behavior

Fluid behaves as viscoplastic when the existence of a yield stress (τ0) for fluid to deform or flow this τ0 must be exceeded. Conversely, when the externally applied stress is smaller than the yield stress material will deform elastically. On exceeding the magnitude of externally applied stress and it becomes greater than yield stress then flow curve will not pass-through origin it may be non-linear or linear. Here we can explain this behavior as when substance at rest it consists of 3D structure of sufficient rigidity to resist the any external stresses which are less than τ0 but when stress increase than τ0 substance behaves like viscous material and structure breaks down.

Bingham plastic fluid is fluid which for |τxy| > | τ0| has a linear flow curve and has constant plastic viscosity and a yield stress, where plastic viscosity is given by the slope of shear stress versus shear rate curve.

Yield-pseudoplastic is substance which for |τxy| > | τ0| possesses yield stress with flow curve of non-linear nature on linear coordinates.

Figure 6

Mathematical models for viscoplastic behavior

(1) The Bingham Plastic model :

The Bingham equation describes the flow pattern of a fluid with a yield stress and in steady one dimension shear.

             for |τxy| > | τ0B|  

                                  for |τxy| < | τ0B|

τ0B and µB are curve fitting constant irrespective of fluid possesses a true yield stress or not.

(2) The Herschel-Bulkley fluid model

To embrace the non linear flow curve (for |τxy| > | τ0B|), Herschel-Bulkley done the simple generalization of the Bingham plastic model, which is three constant Herschel-Bulkley fluid model. For one dimensional steady shearing motion, Herschel-Bulkley model is given as.

                  for |τxy| > | τ0H|

                                     for |τxy| < | τ0H|

Here m depend upon the value of n. This model provides better fit to some experimental data with the use of third parameter.

(3) The Casson fluid model

This model is two constant model and well described for many foodstuffs and biological materials, especially blood .

       for |τxy| > | τ0C|

                                                              for |τxy| < | τ0C|

For describing the steady shear stress — shear rate behavior of blood, yoghurt, tomato puree, molten chocolate, etc. this model is often used.

1.1 Shear-Thickening or Dilatant Behaviors

https://images.app.goo.gl/hyx3JzSYbTgZvQi7A

This fluid type is similar to pseudoplastic systems in which they do not exhibit yield stress, but the apparent viscosity of these fluids increases as the shear rate increases, hence it’s called as shear-thickening. 

This leads to the formation of far greater shear stresses than those detected in a pre-dilated sample at low shear rates. The apparent viscosity n(=σ/ϓ) rises rapidly as the rate of shear increases due to this mechanism. The example data for TiO2 suspensions of various concentrations is shown in Figure 8. The lines of slope unity (Newtonian behavior) are included in this illustration for reference. These suspensions clearly demonstrate both shear-thinning and shear-thickening behavior over a wide range of shear rates and/or concentrations.

Shear-thickening behavior can be seen in thick suspensions and pastes of kaolin, TiO2, corn flour in water, and other The currently available limited information (mainly limited to simple shear) implies that the facility law model, eq. (1), with the power-law index (n) absorbing values bigger than unity, can also be approximate information for these systems. Despite the scarcity of rheologic data on such systems, it’s impossible to say with certainty whether or not these materials also exhibit limiting viscosities between 0 and 1.

Figure 7

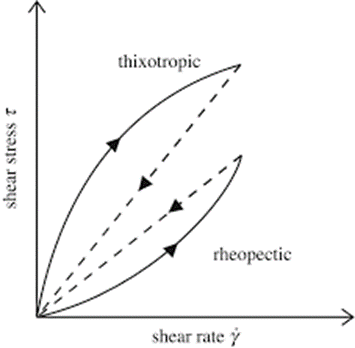
Time Dependent Behavior

In Time Dependent Non-Newtonian Fluid type, viscocity of fluid is dependent on shear rate, temperature and time.

Types Of Time Dependent Fluids :

1) Thixotropy

2) Rheopexy

Figure 8

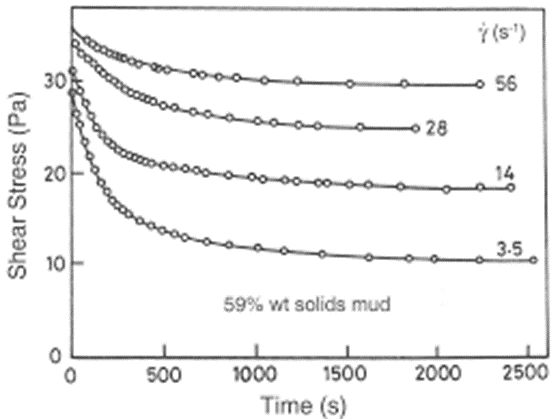
Thixotropy

https://www.indiamart.com/proddetail/castor-oil-15462180291.html

Thixotropy is executed by a material , when at a constant rate it is sheared , its apparent viscosity will decrease with the time of shearing, as can be seen in Figure 1.10 for a red mud suspension performed Nguyen and Uhlherr, 1983.A hysteresis loop is obtained, If the flow curve is measured in a single experiment in which the shear rate is steadily increased at a constant rate from zero to some maximum value and then decreased at the same rate to zero again, shown in Figure 1.11 ; the height, shape and enclosed area of the hysteresis loop rely upon the duration of shearing, the rate of increase/decrease of shear rate and the beyond kinematic history of the sample. No hysteresis loop is found for time-impartial fluids, that is, the enclosed area of the loop is 0. To explain the thixotropic behavior of visco plastic substances. The term ‘false body’ has been added . Although the thixotropy is related to the build-up of form at relaxed state and breakdown of the form below shear, visco plastic substance no longer lose their solid-like prop’s absolutely and can still execute a yield stress, though this is commonly much less than the o authentic cost of the virgin pattern that is regained (if at all) only after a long healing period.

Figure 9

Rheopexy or Negative Thixotropy

https://images.app.goo.gl/5B9dZSoCNFQ92hoq9

liquids or gases whose viscosity  increases with stress by time are Rheopectic fluids . The behavior of these fluids can also be known  as a time-dependent dilatant behavior. Thus, these fluids are a rare class of non-Newtonian fluids. Also, they show an increased viscosity upon agitation. That means, when the fluid is shaken, it becomes thick, or it may even solidify. Moreover, higher the shear stress, more viscous that fluid becomes. It is because the microstructure of these rheopectic fluids is constructed under continuous shearing. Therefore, it is named as shear-induced crystallization. Some common examples of rheopectic fluids include some gypsum pastes, printer ink, lubricants, etc.